JEE 2018 :: Physics (2018) :: Solved questions 2018

• Physics (2018) - Solved questions 2018

A solid sphere of radius r made of a soft material of bulk modulus K is surrounded by a liquid in a cylindrical container. A massless piston of area a floats on the surface of the liquid, covering entire cross- section of cylindrical container. When a mass m is placed on the surface of the piston to compress the liquid, the fractional decrement in the radius of the sphere, ($\frac{\text{d}r}{\text{}r}$) is

Answer:

Explanation:

$\therefore$   Bulk modulus.

 K= $\frac{Volumetric stress }{Volumetric strain} =\frac{\triangle p}{\frac{\triangle v}{v}}$

$\Rightarrow K=\frac{mg}{a(\frac{3\triangle r}{r})} [\therefore V=\frac{4}{3}\pi r^{3}, so \frac{\triangle V}{V}=\frac{3\triangle r}{r} ]$

$\Rightarrow $             $\frac{\triangle r}{r}=\frac{mg}{3aK}$

From a unifrom circular disc of radius R and mass 9 M, a small disc of radius $\frac{R}{3}$ is removed as shown in the figure. The moment of inertia of the remaining disc about an axis perpendicular to the plane of the disc and passing through centre of disc is

Answer:

Explanation:

Moment of inertia of remaining solid =Moment of intertia of complete solid- Moment of inertia of removed portion

$\therefore$  $I=\frac{9MR^{2}}{2}-[ \frac{M(\frac{R}{3})^{3}}{2} +M(\frac{2R}{2})^{2} ]$

  $\Rightarrow I=4MR^{2}$

In a collinear collision, a particle with an initial speed v₀ strikes a stationary particle of the same mass. If the final total kinetic energy is 50% is greater than the  orginal kinetic energy, the magnitude of the relative velocity between the two particles after collision ,is

Answer:

Explanation:

Key idea: Momentum is conserved in all type of collisions,

Final kinectic energy is 50% more than initial kinetic energy

$\Rightarrow\frac{1}{2}mv_{2}^{2}+\frac{1}{2}mv_{1}^{2}\Rightarrow\frac{150}{100}\times\frac{1}{2}mv_{0}^{2}.....(i)$

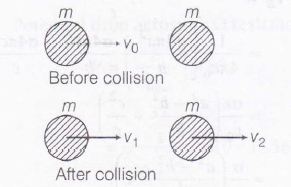
Conservation of momentum gives,

$mv_{0}=mv_{1}+mv_{2}$

$v_{0}=v_{1}+v_{2}......(ii)$

From eq.(i) and (ii), we have

$v_{1}^{2}+v_{2}^{2}+2v_{1}v_{2}=v_{0}^{2}$

$\Rightarrow2v_{1}v_{2}=\frac{-v_{0}^{2}}{2}$

$\therefore (v_{1}^{2}-v_{2}^{2})^{2}=(v_{1}^{2}
+v_{2}^{2})^{2}-4v_{1}v_{2}=2v_{0}^{2}$

or               $v_{rel}=\sqrt{2}v_{0}$

A particle is moving with a uniform speed in a circular orbit of radius R in a central force inversely proportional to the n th power of R. If the period of rotation of the particle is T, then 

Answer:

Explanation:

Force = Mass $\times$ Acceleration = $m\omega^{2}R$

and given ,  $ F\propto\frac{1}{R^{n}}\Rightarrow F=\frac{k}{R^{n}}$

 So, we have

     $\frac{k}{R^{n}}=m (\frac{2\pi}{r})^{2}\times R$

    $T^{2}=\frac{4\pi^{2}m}{k} R^{n+1} \Rightarrow T\propto R^{\frac{n+1}{2}}$

 A particle is moving in a circular path of radius a under the action of an attractive potential  $U=-\frac{k}{2r^{2}}$ , Its total energy is

Answer:

Explanation:

 Force = $-\frac{\text{d}U}{\text{d}r}$

$\Rightarrow   F=-\frac{\text{d}}{\text{d}r}(\frac{-k}{2r^{2}})=$ $-\frac{k}{r^{3}}$

As particle is on circular path, this force must be centripetal force.

$\Rightarrow    \mid F \mid=\frac{mv^{2}}{r}$

So, 

$\frac{k}{r^{3}}=\frac{mv^{2}}{r}\Rightarrow\frac{1}{2}mv^{2}=\frac{k}{2r^{2}}$

 Total energy of particle = KE +PE

  = $\frac{k}{2r^{2}}-\frac{k}{2r^{2}}=0$

Total energy =0

• Physics (2018) - Solved questions 2018